반응형
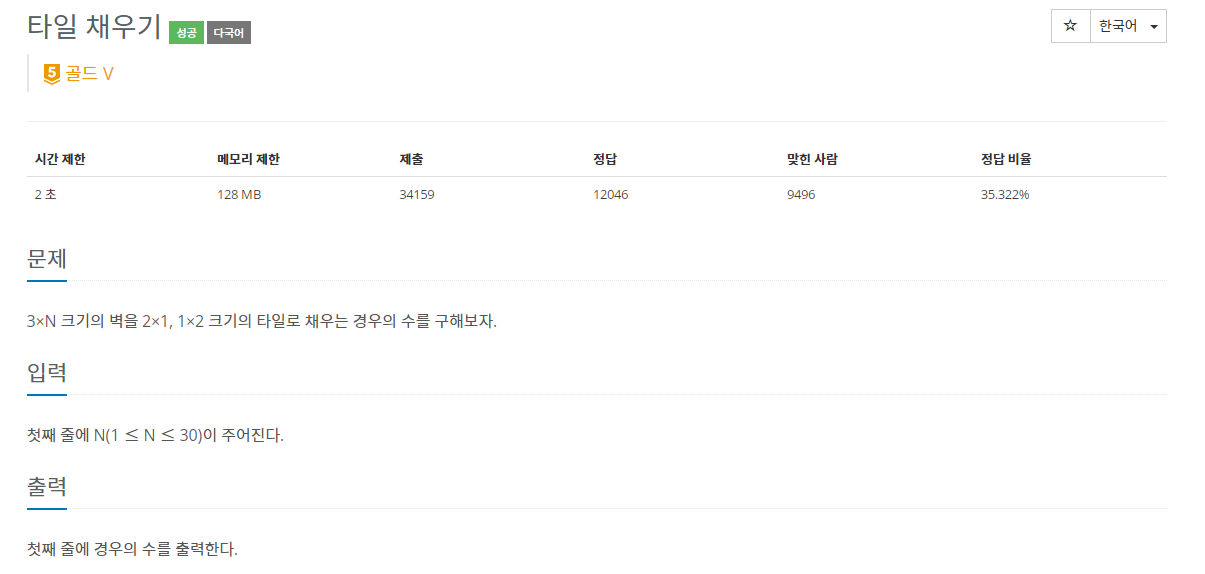
다시한번 타일채우기.
이건 좀 특이한 타일채우기이다.
그래도 여타 타일채우기가 그렇듯, 역시 어렵다.
특이한 점은 이건 홀수일때 0이라는 점이다.
n=2일때를 보자.
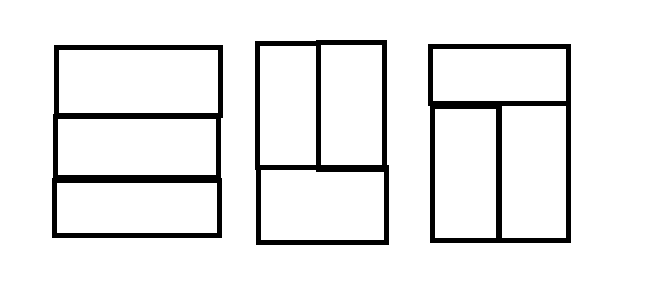
n=3일때는 칸을 다 채울수 없으므로 n=4를 보면,
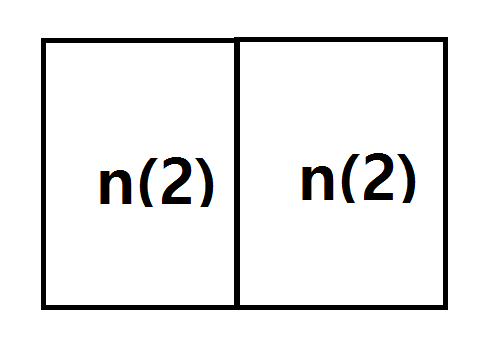
이렇게 쪼개서 생각 할 수 있다. 그리고 여기에 새로운 모양이 생기는데 바로,
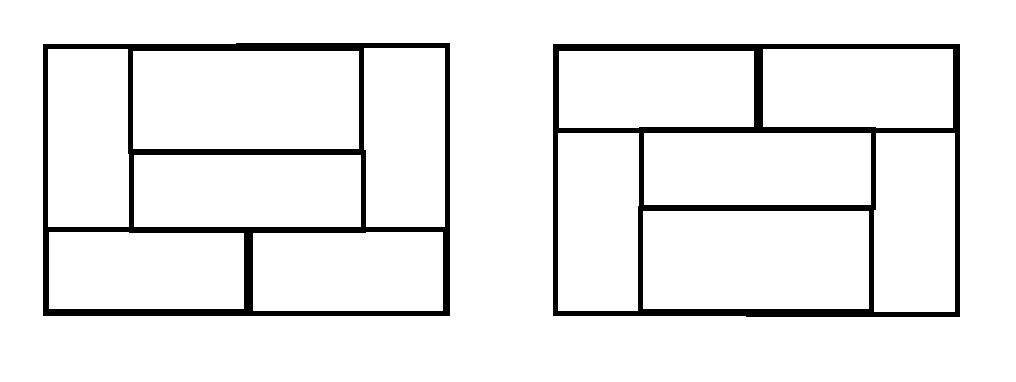
이 두가지이다.
그래서 n(4)=3*n(2)+2=11임을 알 수 있다.
다음은 6이다.
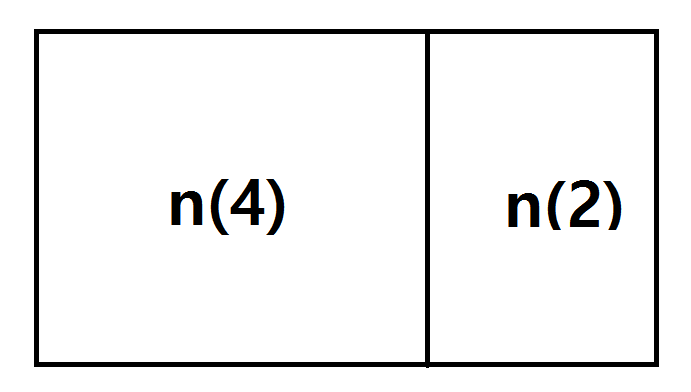
마찬가지로 이렇게 볼 수 있다. 그리고 뒤집으면
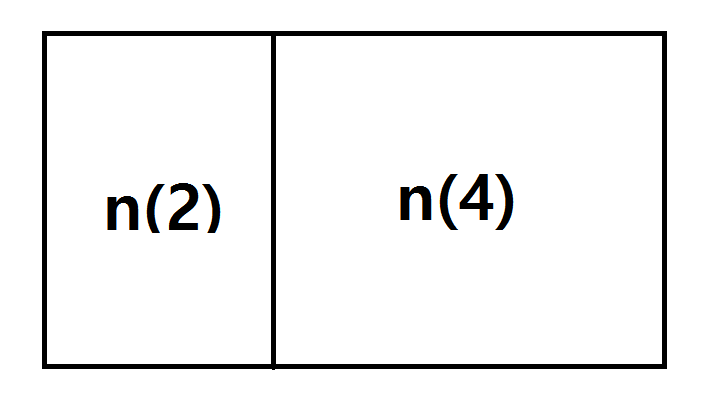
이렇게 되는데, 여기서 세주면 전부 겹치고, 아까 n(4)에서 새롭게 만들어진 두개만 카운트 된다는 것을 알 수 있다.
그리고 n(6)의 새로운 모양도 생긴다.
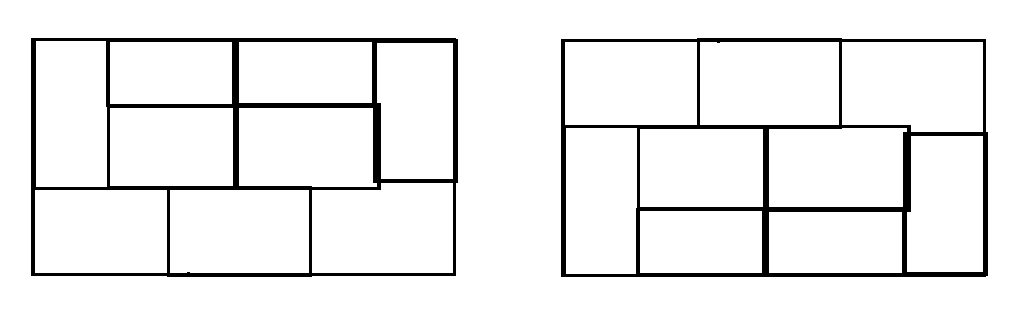
그리고 n=8일때, 경우를 나눠보면 이 세가지인데
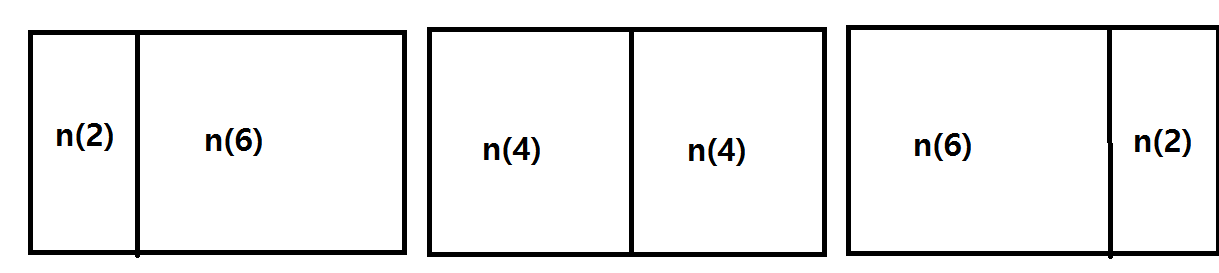
이를 통해서
n(8)=n(2)*n(6)+2(새로생긴 모양)*(n(4)+n(2))임을 알 수 있다.
이러면 일반항을 구할 수 있는데,
n(k)=3*n(k-2)+2(n(k-4)+n(k-6)....k가 2일때까지)+2로 보인다.
그런데 dp[0]=1이므로,
일반항은
n(k)=3*n(k-2)+2*(n(k-4)+n(k-6)....n(0))이다.
n=int(input())
dp=[0 for x in range(n+1)]
dp[0]=1
for x in range(2,n+1):
if x%2==0:
dp[x]=3*dp[x-2]+2*sum(dp[:x-2])
print(dp[n])
반응형
