반응형
0부터 n까지의 정수 k개를 더해서 n이 되는 경우의 수를 구하는 프로그램
뭔가 고등학교 시절의 자연수 분할이 떠오른다. 차이점은 0도 포함한다는 점
예를들어 0부터 9까지 2개로 나타내면
0+0
1+0, 0+1
2+0, 1+1, 0+2
3+0, 1+2, 2+1, 0+3
4+0, 1+3, 2+2, 3+1, 4+0
5+0, 1+4, 2+3, 3+2, 4+1, 5+0
...
와 같이 (n,2)=n+1임을 알 수있다.
그리고 잘 보면, 1+ n-1, 2+n-2꼴로 나타 낼 수 있는데, 이를 잘 보면
(n,k)=(n-1,k-1)+(n-1,k-2)...(n-1,0)으로 나타낼 수 있음을 알 수 있다.
가로는 숫자, 세로는 k개로 나타 낸 것이다
| 0 | 1 | 2 | 3 | 4 | |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 3 | 4 | 5 |
| 3 | 1 | 3 | 6 | 10 | 15 |
| 4 | 1 | 4 | 10 | 20 | 35 |
이 표를 잘 보면
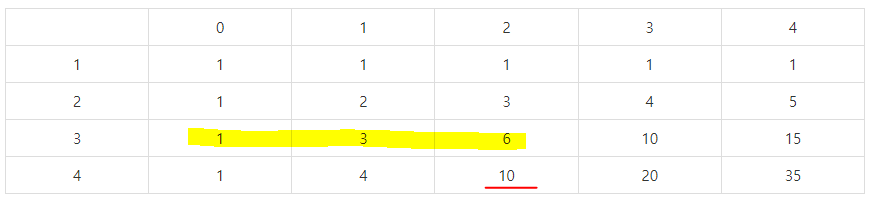
위의 관계식이 맞는 것을 알 수 있다.
그리고 여기서 하나를 더 찾을 수 있는데,

형광펜 그은 부분의 합이 빨강 동그라미와 동일하므로 빨강 동그라미 + 파랑동그라미 = 검정이라는 식이 성립하게 된다.
2차원 배열로 코드를 작성하면 다음과 같다.
ans=0
n,k=map(int,input().split())
dp=[[0 for x in range(n+1)] for x in range(k+1)]
for t in range(k+1):
dp[t][0]=1
for t in range(n+1):
dp[1][t]=1
for x in range(2,k+1):
for y in range(1,n+1):
dp[x][y]=(dp[x-1][y]+dp[x][y-1])%1000000000
print(dp[-1][-1]%1000000000)
반응형
